Disjoint Sets
Operations
union(S1, S2)- return union of $S_1$ and $S_2$
find(S, x)- find the “representative member” (determined by some rule) of the set that $x$ belongs to
Let $\sigma$ be the procedure of $n - 1$ unions and $m \geq n$ finds
Naive implementations
Linked List
- one list per set
- for each list, store pointers to head and tail
- this way,
unionis fast
- this way,
- finding representative takes $\mathcal O(n)$ time
Augmented Linked List
- each element stores pointer to its representative
- this way,
findis fast
- this way,
unionis slow because it must now change $\mathcal O(min(\vert S_1\vert , \vert S_2\vert ))$ pointers to the new representative
Forest (tree-like)
- each set is a tree
- root of a tree is representative of set
- non-root nodes point to a parent node
findworks by ascending the tree until it reaches the root- it takes $\mathcal O(h)$ time where $h$ is height of tree
unionis fast because we must only change one parent pointer - make one tree’s root point to an element of other tree- to support this, record size (number of nodes) for each tree
Weighted Union
To do union, make root of smaller tree point to root of larger tree
Lemma
With weighted union, any tree $T$ of height $h$ created during the execution of $\sigma$ has $\vert T\vert \geq 2^h$
Proof.
Base case:
If $h = 0$, then the tree has $1 = 2^0$ node
Inductive step:
Suppose lemma holds for some $h \geq 0$.
To construct a tree of height $h+1$, we make the root of a tree $A$ of height $h$ point to the root of a bigger tree $B$ (because we are using weighted union)
By IH, $\vert A\vert \geq 2^h$
By WU rule, $\vert B\vert \geq \vert A\vert \geq 2^h$
Then resulting tree has number of nodes $\vert A\vert + \vert B\vert \geq 2 (2^h) = 2^{h + 1}$
Path compression
find(S, x)ascends tree until root is reached- intermediate nodes $n_1, …, n_m$ on way to root do not matter, so after we find
rootwe can changen.parent = rootfor each $n$ on the way to the root (as well asx.parent = root
Before:
find(S, x) traverses from x to root
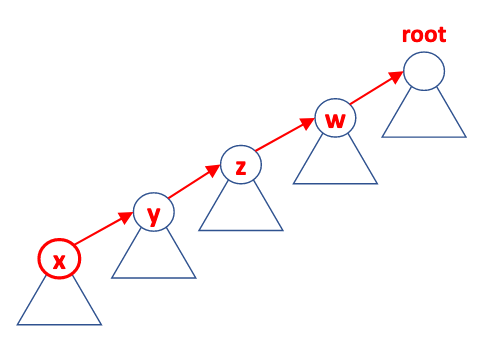
After:
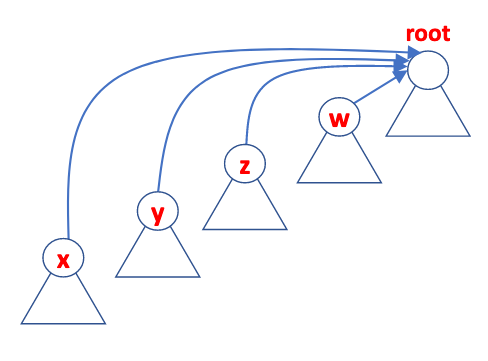
- this does not increase complexity, as same nodes must be operated on twice, aka a constant factor difference
- speeds up subsequent calls to
findonxor any of its ancestors - becomes constant time- does not affect time for
findon other parts of the tree, does not affectunionat all
- does not affect time for
History: 25 years after publication of weighted union + path compression implementation, proof that $\sigma$ takes $\Theta(m \cdot \alpha(m, n))$ time using WU+PC was finally completed (where $\alpha$ is inverse Ackerman function).
The Ackerman function grows ridiculously quickly so $\alpha$ grows ridiculously slowly, so for all reasonable (read: physically possible) intents, $\sigma$ runs in linear time.